Использование GNU Octave для инженерных и математических расчётов
Евгений Алексеев, Оксана Чеснокова, Донецк, Украина, Донецкий национальный технический университет
Octave is a powerful program to solve engineering and mathematical problems. Its capabilities include packages for linear algebra, analytic geometry, mathematical analysis. Octave provides rather elaborated plotting. Octave can be used to solve differential equations, optimization problems and problems of processing the experiment data, occurring frequently in engineering and scientific practices.
Среди свободных математических программ наиболее известными являются Scilab и Maxima. Достойным конкурентом им может быть программа GNU Octave. Octave представляет собой интерактивный командный интерфейс для решения математических задач. Octave – это мощный математический язык интерпретирующего типа. Интерпретатор Octave входит в состав многих дистрибутивов Linux (Debian, Ubuntu, Mandriva, ALT Linux), есть версия и для ОС Windows.
Существуют и графические оболочки для работы с Octave (QtOctave, Xoctave), однако главным достоинством Octave является мощный математический язык интерпретирующего типа, а также наличие постоянно пополняющегося репозитария пакетов расширений octave-forge (http://octave.sourceforge.net).
В Octave встроен язык программирования, очень близкий к языку проприетарной программы Matlab, позволяющий реализовать алгоритм любой сложности.
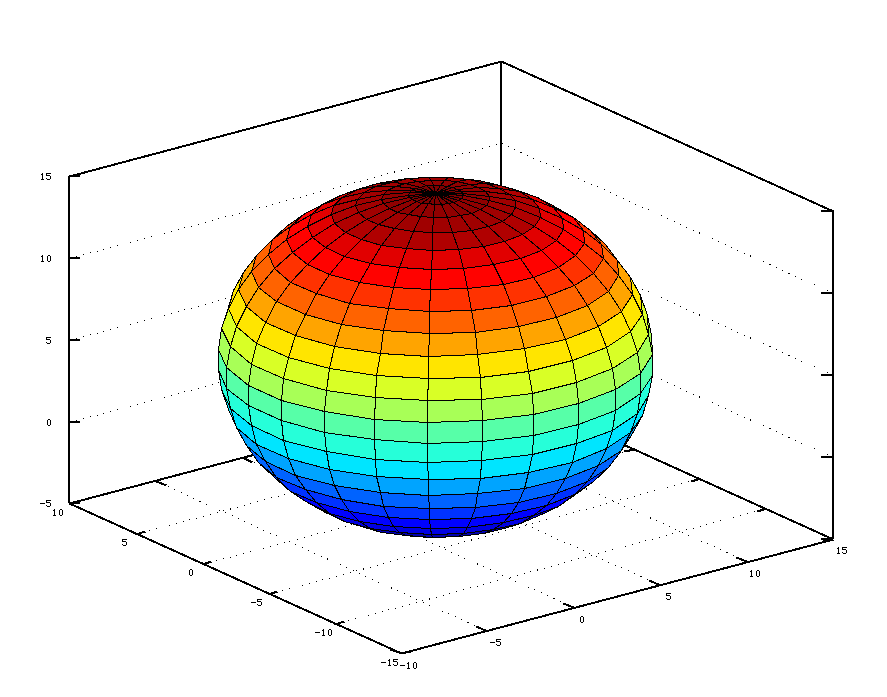
Функции Octave позволяют создавать графики и поверхности различной сложности. Для построения двумерных графиков можно использовать функции plot и fplot, полярные графики строятся с помощью встроенной функций polar, функции mesh(x,y,z), surf(x,y,z) позволяют строить поверхности различного вида. По умолчанию для построения графиков и поверхностей в Octave используется пакет gnuplot (http://www.gnuplot.info), который может использоваться и как самостоятельная программа для построения графиков.
Графики графики нескольких функций в одном окне:
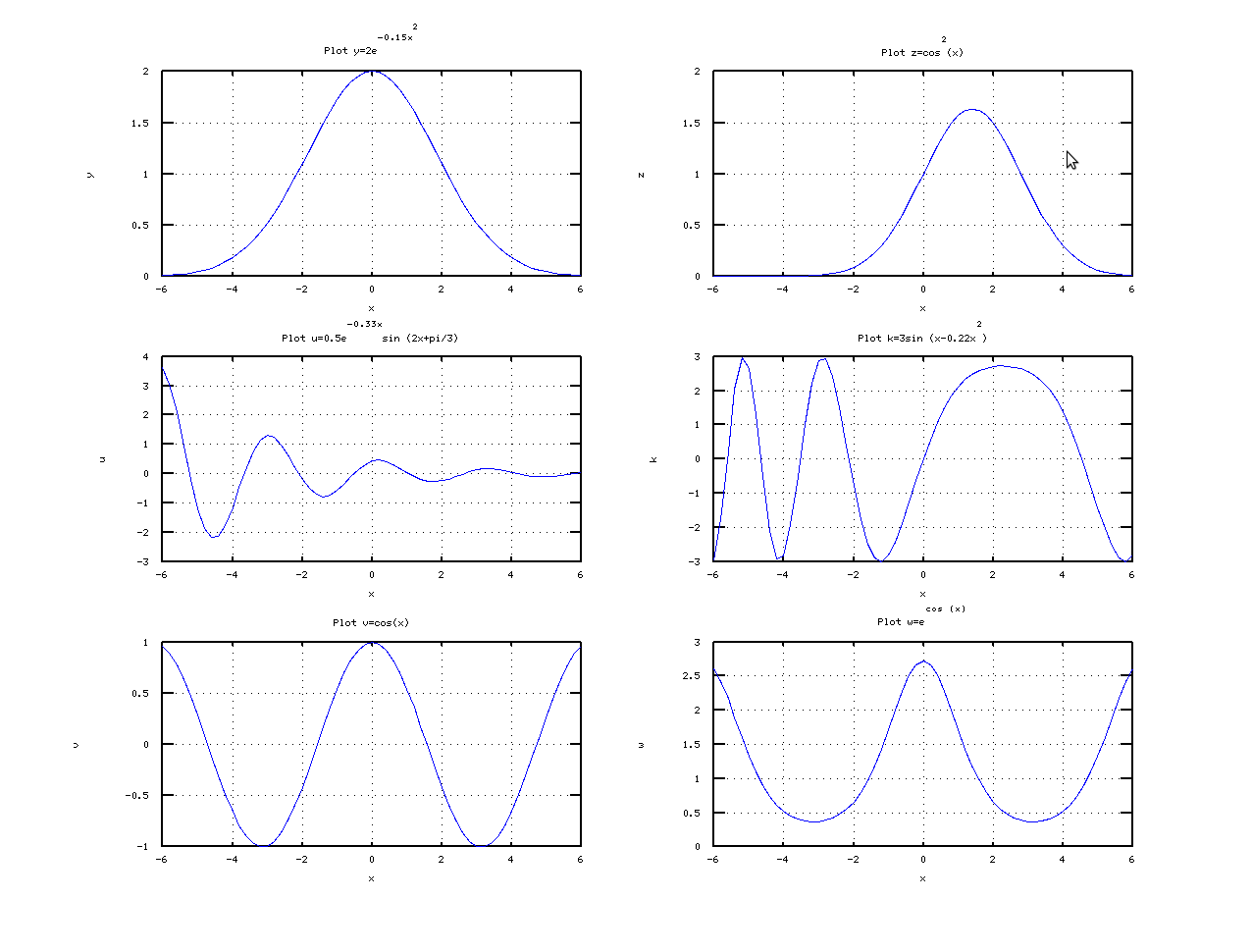
Графики архимедовой, гиперболической и логарифмической спирали, окружности в полярных координатах:
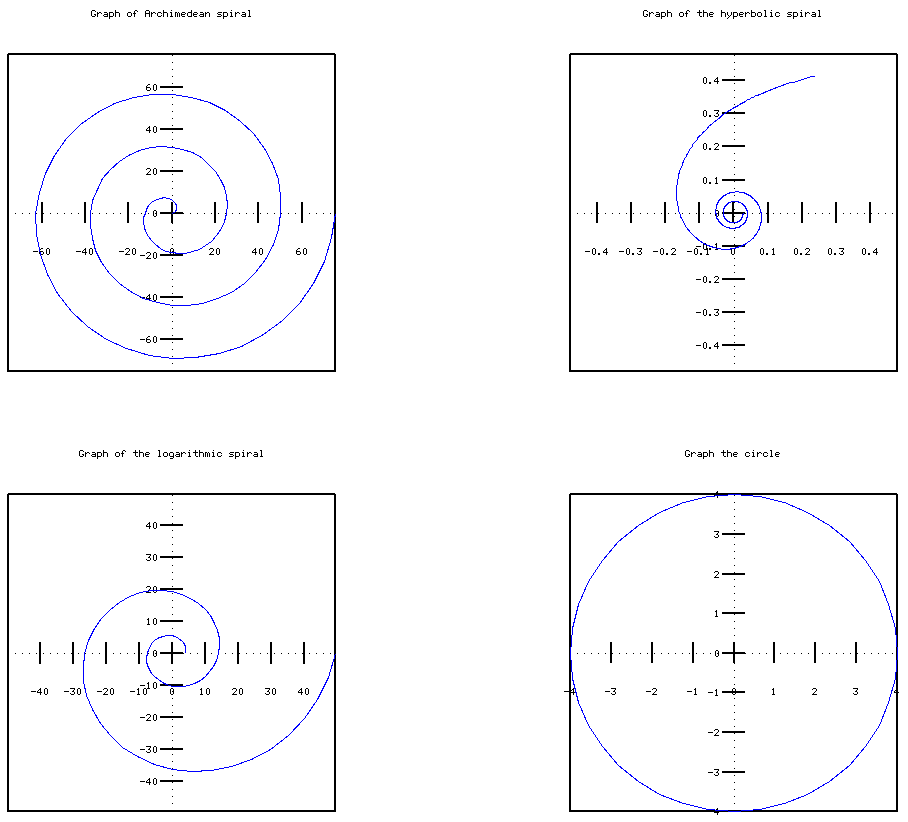
Octave содержит большое количество функций, предназначенных для решения задач линейной алгебры, наиболее используемые из них: det(M) – вычисляет определитель квадратной матрицы M, norm(M[,p]) – возвращает различные виды норм матрицы M в зависимости от p, inv(M) – возвращает матрицу обратную к M, eig(M) – возвращает вектор собственных значений матрицы M, rref(M) – осуществляет приведение матрицы M к треугольной форме, используя метод исключения Гаусса, lu(M), qr (M) – выполняют LU и QR-разложение соответственно.
Мощная графическая и математическая база Octave позволяет решать задачи векторной алгебры и аналитической геометрии.
Octave содержит функции для численного и аналитического решения нелинейных уравнений и систем, а также для интегрирования и дифференцирования.
Оптимизационные задачи чаще всего решают с помощью проприетарного табличного процессора MS Excel. Однако, наиболее мощные и гибкие функции для решения подобных задач присутствуют именно в Octave. Так, для решения линейных и нелинейных оптимизационных задач с ограничениями можно использовать функцию sqp, а для решения любых задач линейного программирования есть функция glpk. Сложные оптимизационные задачи в Octave решают с помощью пакета пакета расширений Minimization для GNU Octave (http://octave.sourceforge.net/optim/overview.html).
В инженерной практике часто приходится сталкиваться с решением обыкновенных дифференциальных уравнений и систем. В Octave существует достаточно много функций для решения обыкновенных уравнений и систем (в том числе и жёстких). Наиболее часто используемые среди них:
- ode23, ode45 – функции решений обыкновенных нежёстких дифференциальных уравнений (или систем) методом Рунге-Кутта 2-3-го и 4-5-го порядка точности соответсвенно,
- ode5r, ode2r – функции решений обыкновенных жёстких дифференциальных уравнений (или систем).
Графики точного решения (-) дифференциального уравнений и решения (*), найденного с помощью ode23:
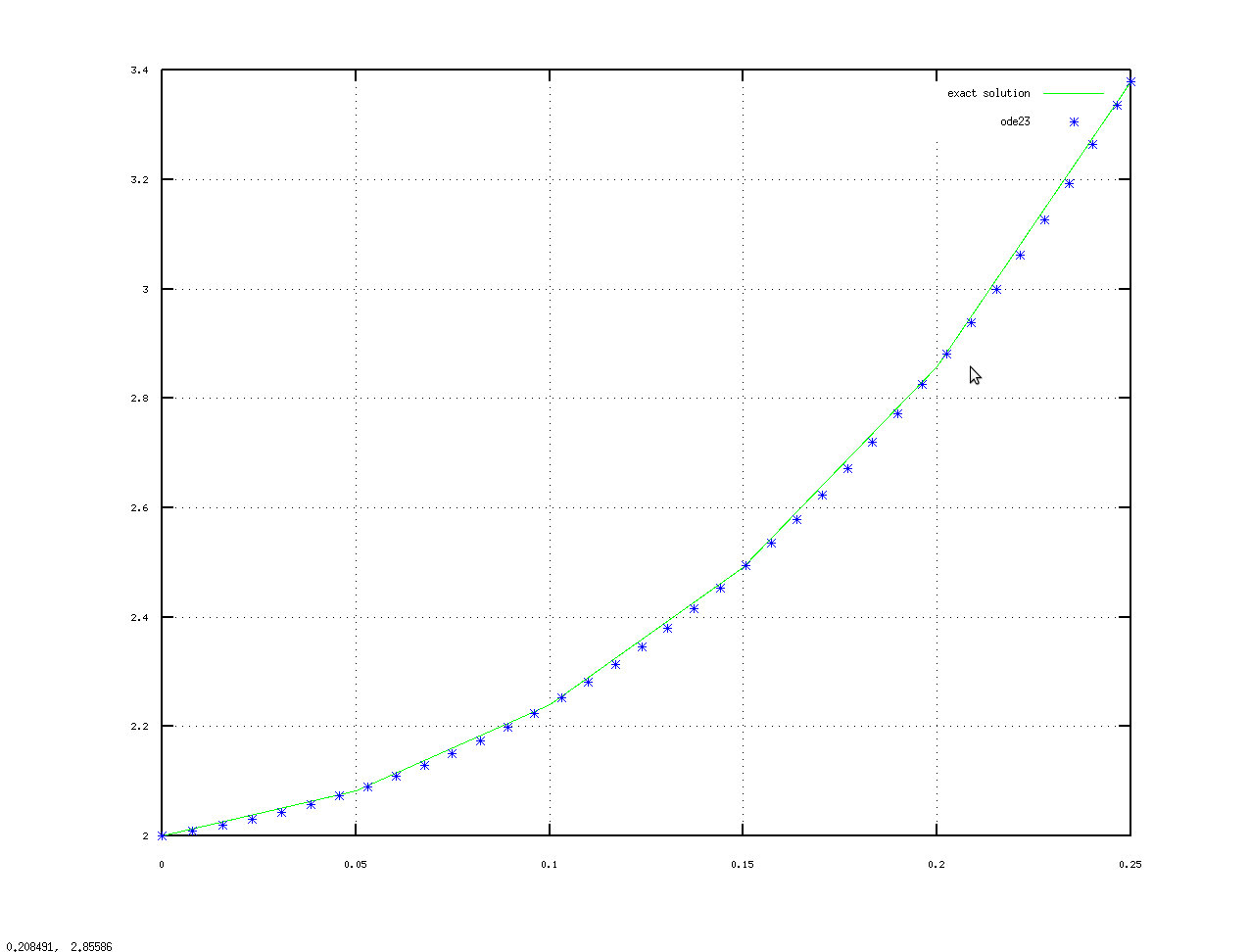
Множество функций для решения дифференциальных уравнений находится в пакете расширений odepkg. Краткое описание функций этого пакета на английском языке с некоторыми примерами приведено на странице http://octave.sourceforge.net/odepkg/overview.html.
Также в Octave можно решать практически любые задачи обработки эксперимента. Для подбора параметров аналитической зависимости методом наименьших квадратов используются следующие функции: polyfit – подбор коэффициентов полинома k-й степени; sqp – функция поиска минимума.
Сплайн-интерполяция в Octave реализуется с помощью функции interp1, которая позволяет построить кубический и линейный сплайн.
C помощью Octave можно решать и много других задач. Авторами подготовлен учебник по использованию пакете GNU Octave, который будет опубликован в ближайшее время в Москве, в серии учебников ALT Linux, а также небольшим тиражом в Донецком национальном техническом университете. Рабочие материалы книги можно увидеть на сайте http://gnu-octave.narod2.ru.
Рассмотренные возможности Octave позволяют авторам рекомендовать пакет как инструмент для решения математических задач в курсах «Высшая математика», «Математический анализ», «Линейная алгебра», «Аналитическая геометрия», а также во многих специальных курсах, в которых приходится решать задачи вычислительной математики.